Two Dimensional Transformations

Two Dimensional Geometric Transformations

Changes in orientations, size and shape are accomplished with geometric transformations that alter the coordinate description of objects.

Basic Transformation 

Translation

A translation is applied to an object by representing it along a straight line path from one coordinate location to another adding translation distances, tx, ty to original coordinate position (x, y)to move the point to a new position (x’, y’) tox’ = x + tx, y’ = y + ty

The translation distance point (tx, ty) is called translation vector or shift vector. Translation equation can be expressed as single matrix equation by using column vectors to represent the coordinate position and the translation vector as

x' = x + t_x

y' = y + t_y

= +

P' = P + T

Moving a polygon from one position to another position with the translation vector (-5.5, 3.75)

Rotations:

A two dimensional rotation is applied to an object by repositioning it along a circular path on xy plane. To generate a rotation, specify a rotation angle θ and the position (xr, yr) of the rotation point (pivot point)about which the object is to be rotated.

Positive values for the rotation angle define counter clock wise rotation about pivot point. Negative value of angle rotates objects in clock wise direction. The transformation can also be described as a rotation about a rotation axis perpendicular to xy plane and passes through pivot point.

Rotation of a point from position(x, y) to position (x’, y’) through angle θ relative to coordinate origin

The transformation equations for rotation of a point position P when the pivot point is at coordinate origin. In figure r is constant distance of the point positions Ф is the original angular of the point from horizontal and θ is the rotationangle. The transformed coordinates in terms of angle θ and Ф

x’ = rcos(θ+Ф) = rcosθosФ – rsinθsinФ y’ = rsin(θ+Ф) = rsinθcosФ + rcosθsinФ

The original coordinates of the point in polar coordinates x =rcosФ, y = rsinФ

The transformation equationfor rotating a point at position (x,y) through an angle θ

about origin

x’ = xcosθ – ysinθy’ = xsinθ + ycosθ

Rotation Equation

Rotation Matrix R=𝑐𝑜𝑠∅  −𝑠𝑖𝑛∅

𝑠𝑖𝑛∅      𝑐𝑜𝑠∅

P’ = R

Note: Positive values for the rotation angle define counterclockwise rotations about the rotation point and negative values rotate objects in the clockwise.

Scaling

A scaling transformation alters the size of an object. This operation can be carried out for polygons by multiplying the coordinate values (x, y) to each vertex by scaling factor Sx&Sy to produce the transformed coordinates (x’, y’) scaling factor Sx scales object in x direction while Sy scales in y direction. The transformation equation in matrix form

x’=x.Sx                          y’ =y.Sy

𝑥′  𝑆𝑥 0      𝑥

𝑦′= 0 𝑆𝑦 . 𝑦(or)

P’ = S. P

Where S is 2 by 2 scaling matrix

Turning a square (a) Into a rectangle (b) with scaling factors sx = 2 and sy = 1.Any positive numeric values are valid for scaling factors sx and sy. Values less than 1 reduce the size of the objects and values greater than 1produce an enlarged object.

There are two types of Scaling. They are

• Uniform scaling
• Non Uniform Scaling

To get uniform scaling it is necessary to assign same value for sx and sy. Unequal values for sx and sy result in a non uniform scaling.

Matrix Representation and Homogeneous Coordinates

Many graphics applications involve sequences of geometric transformations. An animation, for example, might require an object to be translated and rotated at each increment of the motion. In order to combine sequence of transformations we have to eliminatethematrixaddition.Toachievethiswehaverepresentmatrixas3X3insteadof2X2introd using an additional dummy coordinate. Here points are specified by three numbers instead of two. This coordinate system is called as Homogeneous coordinate system and it allows expressing transformation equation as matrix multiplication. Cartesian coordinate position (x, y) is represented as homogeneous coordinate triple(x,y, h)

• Represent coordinates as (x, y,h)
• Actual coordinates drawn will be (x/h,y/h)

Composite Transformations

Acompositetransformationisasequenceoftransformations;onefollowedbytheother. We can setup a matrix for any sequence of transformations as a composite transformation matrix by calculating the matrix product of the individual transformations.

Translation

If two successive translation vectors (tx1,ty1) and (tx2,ty2) are applied to a coordinate position P, the final transformed location P’ is calculated as

P’ = T(tx2, ty2). {T(tx1, ty1).P}

= {T(tx2, ty2).T(tx1,ty1)}.

Where P and P’ are represented as homogeneous-coordinate column vectors.

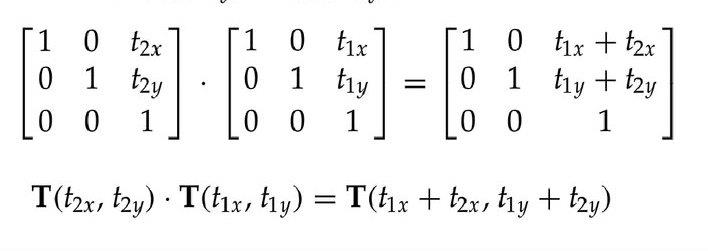
Which demonstrated the two successive translations are additive.

Rotations

Two successive rotations applied to point P produce the transformed position

P’ = R(θ2).{R(θ1).P} = {R(θ2).R(θ1)}.P

By multiplying the two rotation matrices, we can verify that two successive rotation are additive

R(θ2).R(θ1) = R(θ1 + θ2)

So that the final rotated coordinates can be calculated with the composite rotation matrix as P’ = R(θ1 + θ2).P

Scaling

Concatenating transformation matrices for two successive scaling operations produces the following composite scaling matrix.

General Pivot-Point Rotation

1. Translate the object so that pivot-position is moved to the co-ordinate origin
2. Rotate the object about the co-ordinate origin

Translate the object so that the pivot point is returned to its original position

The composite transformation matrix for this sequence is obtain with the concatenation Which can also be expressed as T(xr, yr).R(θ).T(-xr, -yr) = R(xr, yr, θ)

General fixed point Scaling

1. Translate object so that the fixed point coincides with the  co-ordinate origin
2. Scale the object with respect to the co-ordinate origin

Use the inverse translation of step 1 to return the object to its original position

Concatenating the matrices for these three operations produces the required scaling matrix Can also be expressed as 

T(xf, yf).S(sx, sy).T(-xf, -yf) = S(xf, yf, sx, sy)

Note: Transformations can be combined by matrix multiplication

Other Transformations

1. Reflection
2. Shear