Dijkestra's Algorithm

Dijkstra's algorithm - is a solution to the single-source shortest path problem in graph theory. Works on both directed and undirected graphs. However, all edges must have nonnegative weights.

Approach: Greedy

Input: Weighted graph G={E,V} and source vertex v∈V, such that all edge weights are nonnegative.

Output: Lengths of shortest paths (or the shortest paths themselves) from a given source vertex v∈V to all other vertices.

Pseudocode

dist[s] ←0 						(distance to source vertex is zero)
for all v ∈ V–{s}
 do dist[v] ←∞ 					(set all other distances to infinity)
S←∅ 							(S, the set of visited vertices is initially empty)
Q←V 							(Q, the queue initially contains all vertices)
while Q ≠∅ 						(while the queue is not empty)
do u ← mindistance				(Q,dist) (select the element of Q with the min. distance)
 S←S∪{u} 						(add u to list of visited vertices)
 for all v ∈ neighbors[u]
 do if dist[v] > dist[u] + w(u, v) 			(if new shortest path found)
 then d[v] ←d[u] + w(u, v) 					(set new value of shortest path)
	(if desired, add traceback code)
return dist

Animated Example

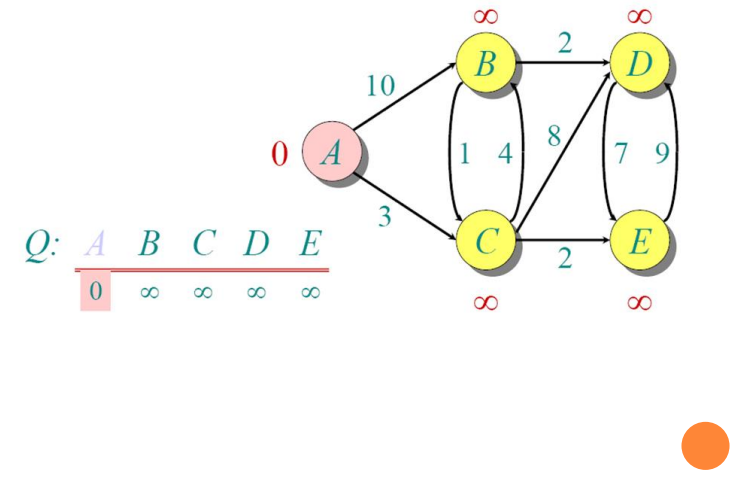
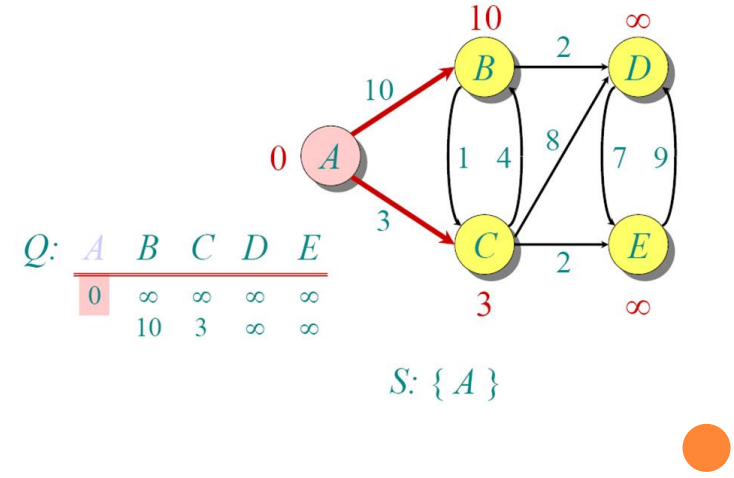
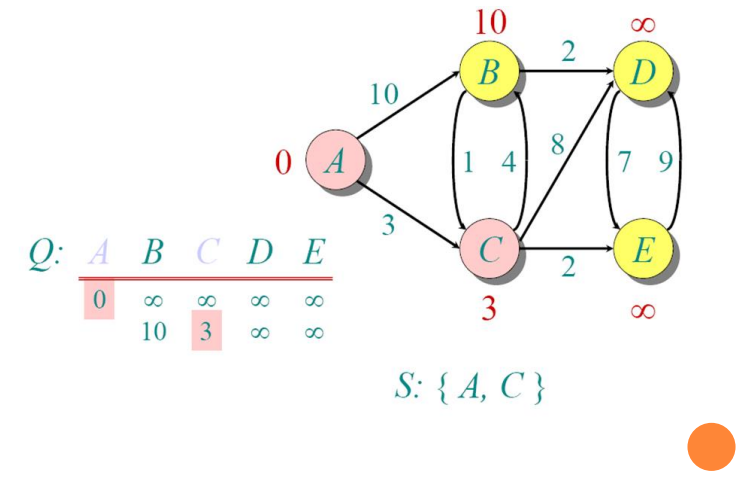
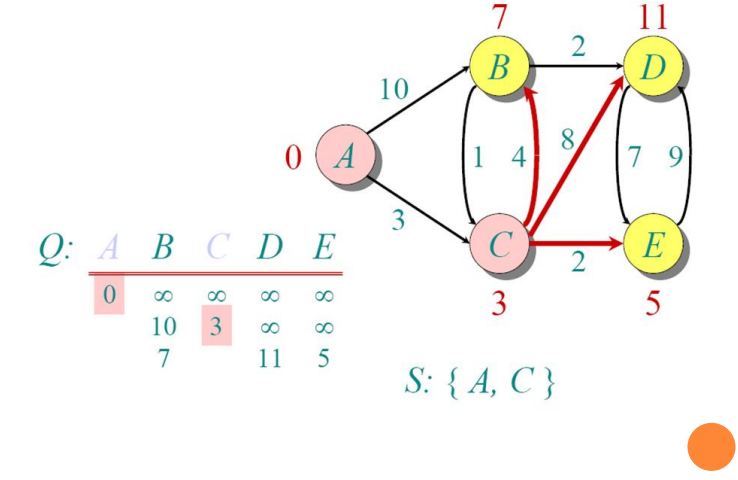
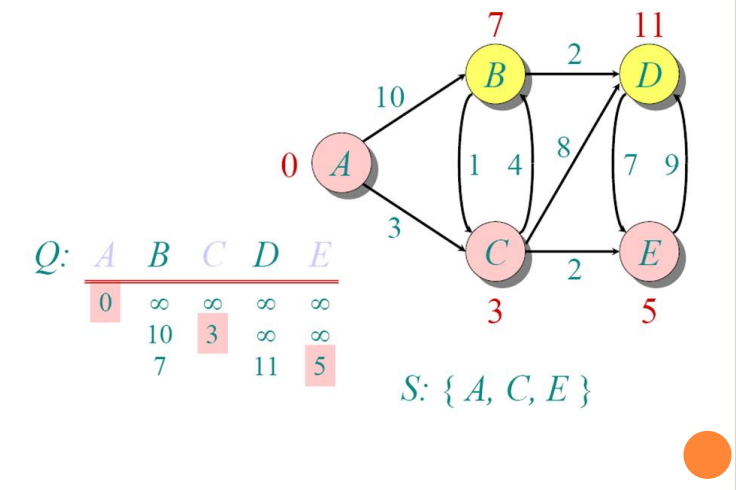
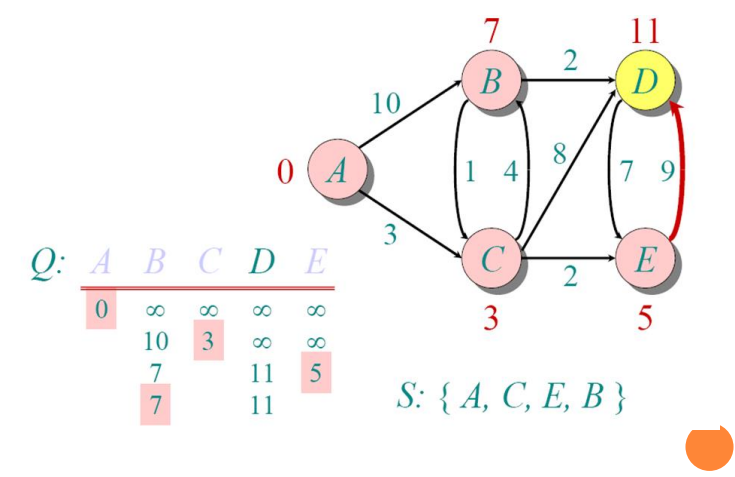
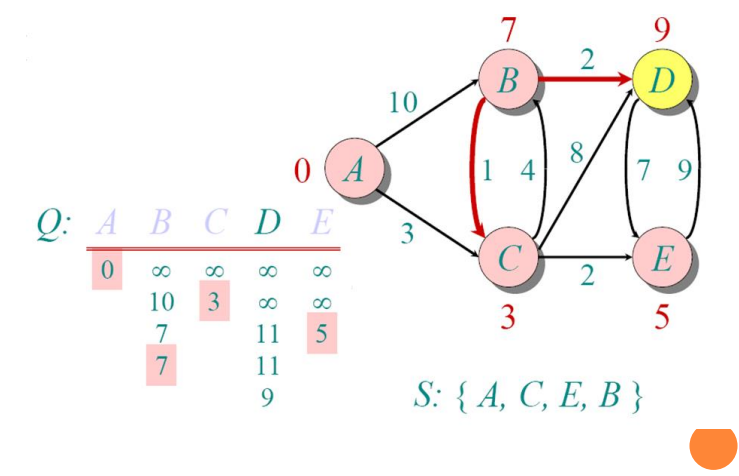
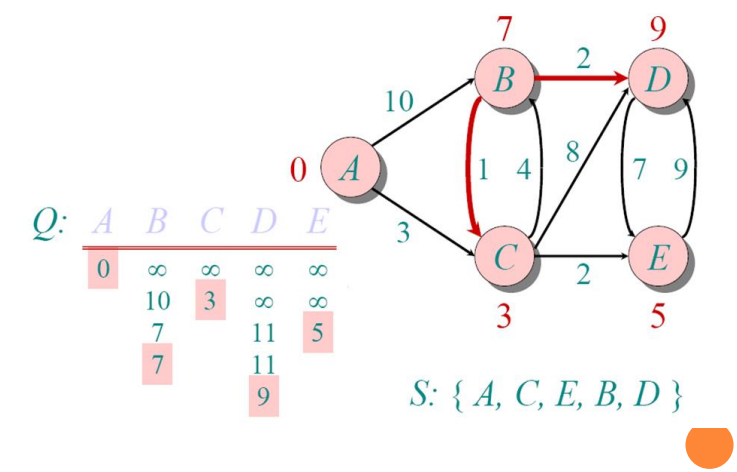
Implementations and Running Times

The simplest implementation is to store vertices in an array or linked list. This will produce a running time of

O(|V|^2 + |E|)

For sparse graphs, or graphs with very few edges and many nodes, it can be implemented more efficiently storing the graph in an adjacency list using a binary heap or priority queue. This will produce a running time of

O((|E|+|V|) log |V|)

Why It Works

As with all greedy algorithms, we need to make sure that it is a correct algorithm (e.g., it always returns the right solution if it is given correct input).
A formal proof would take longer than this presentation, but we can understand how the argument works intuitively.
If you can’t sleep unless you see a proof, see the second reference or ask us where you can find it.
To understand how it works, we’ll go over the previous example again. However, we need two mathematical results first:
Lemma 1: Triangle inequality If δ(u,v) is the shortest path length between u and v, δ(u,v) ≤ δ(u,x) + δ(x,v)
Lemma 2: The subpath of any shortest path is itself a shortest path.
The key is to understand why we can claim that anytime we put a new vertex in S, we can say that we already know the shortest path to it.
Now, back to the example…

Why Use It?

As mentioned, Dijkstra’s algorithm calculates the shortest path to every vertex.
However, it is about as computationally expensive to calculate the shortest path from vertex u to every vertex using Dijkstra’s as it is to calculate the shortest path to some particular vertex v.
Therefore, anytime we want to know the optimal path to some other vertex from a determined origin, we can use Dijkstra’s algorithm.

Applications

Traffic Information Systems are most prominent use.
Mapping (Map Quest, Google Maps).
Routing Systems.

One particularly relevant this week: epidemiology.
Prof. Lauren Meyers (Biology Dept.) uses networks to model the spread of infectious diseases and design prevention and response strategies.
Vertices represent individuals, and edges their possible contacts. It is useful to calculate how a particular individual is connected to others.
Knowing the shortest path lengths to other individuals can be a relevant indicator of the potential of a particular individual to infect others.

Menu